
Actas del Congreso Nacional de
Tecnología Aplicada a Ciencias
de la Salud



Actas del Congreso Nacional de Tecnología Aplicada a Ciencias de la Salud Vol. 5, 2023
En este trabajo se explora el uso de fractales en el campo de la electrónica, específicamente en las antenas de radiofrecuencia (RF) [1]. Las antenas fractales tienen como objetivo reducir el tamaño de la antena RF y mejorar su rendimiento en los sistemas [2]. Se propone realizar una comparación y análisis de una antena con estructura fractal de triángulo de Sierpinski, que opera en frecuencias previamente investigadas. En la actualidad, la tecnología fractal es considerada una de las mejores opciones para el diseño de este tipo de antenas [3], con las comparaciones entre estas antenas, se puede obtener una comprensión más precisa acerca del uso de las antenas fractales, aprovechando así sus numerosas ventajas. [4].
Palabras claves: Fractales, Antena, Resonancia
In this work, the properties of fractals and their relevance in the field of electronics are mentioned through their application in radiofrequency (RF) antennas [1]. The purpose of fractal antennas is to reduce the size of the RF antenna profile and improve its performance in systems [2]. It is proposed to make a comparison and analysis of an antenna with a Sierpinski triangle fractal structure, operating at previously investigated frequencies. Currently, fractal technology is considered one of the best options for designing this type of antennas [3]. By comparing these antennas, a more accurate understanding of the use of fractal antennas can be obtained, thus taking advantage of their numerous benefits. [4].
Key words: Fractal, Antenna, Resonance
Las antenas fractales se han utilizado ampliamente en el campo de las telecomunicaciones debido a su tamaño compacto y funcionalidad. Este proyecto tiene como objetivo desarrollar antenas fractales multibanda o de banda ancha para su uso en frecuencias de RF [1]. Los sistemas inalámbricos que operan en frecuencias de RF y microondas requieren antenas pequeñas, pero con un ancho de banda amplio [2]. Para abordar esto, se propone una antena fractal basada en la estructura del triángulo de Sierpinski.
El tamaño de una antena limita tanto su ancho de banda como su eficiencia, como indica el físico Harold A. Wheeler en su estudio sobre antenas compactas. La mayoría de las antenas solo pueden operar en una frecuencia específica donde su ganancia es máxima. Sin embargo, las antenas fractales ofrecen una solución compacta y multibanda, capaz de proporcionar altas ganancias en varias frecuencias simultáneamente [5]. Están diseñadas para maximizar la recepción y transmisión de señales en un área determinada.
Los fractales, definidos por Mandelbrot en 1975 [3], exhiben autosimilitud a diferentes escalas de magnificación. La principal ventaja de las antenas fractales es su menor tamaño físico en comparación con las antenas convencionales. Esto es especialmente beneficioso en el campo de la medicina, donde los dispositivos a menudo tienen un tamaño limitado [4]. Al utilizar antenas fractales, se puede maximizar el rendimiento de la comunicación inalámbrica sin ocupar mucho espacio adicional. Esto es crucial para miniaturizar dispositivos médicos y ofrecer soluciones más eficientes y cómodas para los pacientes. Las antenas fractales permiten la integración de la tecnología de comunicación inalámbrica en dispositivos médicos más pequeños, como marcapasos, monitores de salud portátiles e implantes [5].
Este proyecto tiene dos objetivos principales. En primer lugar, tiene como objetivo analizar la geometría de la estructura fractal del triángulo de Sierpinski y el método de construcción más utilizado. En segundo lugar, pretende modelar la densidad de flujo magnético en esta antena fractal utilizando herramientas de modelado y análisis de fenómenos físicos e ingeniería.
La irregularidad del cuerpo humano es una característica evidente dentro de la medicina, Sin embargo, tradicionalmente se ha medido con métricas euclidianas, mediante la aproximación de sus formas a líneas, áreas y volúmenes regulares. Es decir, las medidas no son totalmente confiables y es por esto por lo que se propone la geometría fractal la cual permite caracterizar adecuadamente la forma irregular que existe en el cuerpo humano [4]. Dentro de la literatura se encuentran trabajos previos relacionados con el uso de antenas fractales enfocadas en la medicina, estas investigaciones son de mucha importancia para esta investigación, se mencionan los más relevantes.
En 1990, El físico Bruce J West, de la universidad de Texas, publicó el trabajo titulado “La fisiología fractal y el caos en la medicina”. En este menciona que la aplicación de la dimensión fractal dentro del campo de la medicina había sido de gran importancia en las áreas clínica y experimental, en las que se habían caracterizado objetos como la estructura neuronal y pulmonar, los intestinos y los vasos sanguíneos de diferentes estructuras, entre otros [5].
En 2012, Rogers J, de la universidad de Illinois, publicó su trabajo titulado “Materiales y mecánica para la electrónica flexible”. En el que habla del análisis de las mallas en IRMN sugiriendo que los diseños basados en fractales ofrecen vías para crear dispositivos electrónicos implantados o montados en la piel, como si fueran un tatuaje [6].
De ahí se derivó el trabajo, en 2014, titulado “Conceptos de diseño fractal para la electrónica flexible” en donde mencionaban que a diferencia de las mallas que se usan en resonancia magnética, los fractales no contienen bucles cerrados, no se acoplan a la radiación de RF y según estudios realizados y que posteriormente publicaron en la revista NATURE, son invisibles en la resonancia magnética, es decir que no afectan las imágenes [7].
En 2021, Nowikow publicó el “Análisis de redes y campos de bobinas de radiofrecuencia de geometría fractal de copo de nieve de Koch para resonancia magnética de sodio”, realizando el análisis de red de campo de antenas de RF fractales para resonancia magnética enfocadas en hacer resonar otros núcleos de átomos como el sodio. Estas antenas son de gran utilidad ya que además de tener características fractales, tienen una menor inductancia mutua al ser colocadas en fase [8].
Y por último, en 2023, Lala A., publica el trabajo titulado “Antena miniaturizada para la detección del cáncer de mama en la banda ISM de 5,725,82 GHz basada en la técnica DGS“, en este trabajo investigaron el parámetro del coeficiente de reflexión para detectar el cáncer de mama en diferentes posiciones utilizando tres escenarios una antena sobre el modelo de mama, dos antenas sobre el modelo de mama y un modelo de mama entre dos antenas con una separación de 10 cm. Siendo este último, el mejor escenario, que ofrecía mayor contraste entre las mamas sanas y las afectadas [9].
Las antenas de radio frecuencia utilizadas en la medicina tienen un ancho de banda fijo para poder detectar o enviar señal de forma específica para ciertas frecuencias [10]. Debido a esto surge la necesidad de antenas que sean multibanda o que su ancho de banda sea grande, aquí es donde entran las antenas fractales [11].
La palabra fractal, viene del latín “fractus”, que significa fracturado, roto o irregular [12]. En 1975 Mandelbrot definió un fractal como: “Una Figura hecha de partes similares a la forma completa, es decir, es un objeto que posee simetría a través de la escala bajo diferentes grados de ampliación”. Ya que 8 años antes en 1967 con su publicación “¿cuánto mide la costa de gran bretaña?” [13] había introducido la idea de que “entre más pequeña es la regla con la que se mida un objeto irregular, más cerca se está de saber el verdadero valor de su perímetro”.
Las características principales de un fractal son

Figura 1. construcción del triángulo de Sierpinski (Cardama et al., 2002)
Como se muestra en la figura 1, se tiene un triángulo que se llama el iniciador y el generador que es el triángulo que es eliminado. De este modo se observa la autosimilaridad a medida que se realizan las iteraciones.

Figura 2. Dimensión euclídea y fractal. (García et al., 2010)
Se observa en la figura 2, que debido a que una línea fractal NO abarca toda la porción del plano, no tiene una dimensión entera [15]. La dimensión fractal de un contorno, se calcula mediante el algoritmo de “box counting” que no es más que la medición de las irregularidades del borde con rejillas de diferentes tamaños.
La relación entre la escala R y el número de partes N de un objeto es:
Reescribiendo se tiene la dimensión fractal [15] tenemos la ecuación 4
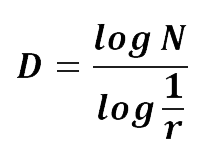
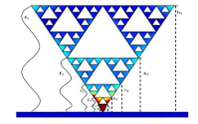
Figura 3. Rangos de frecuencia y de banda de una antena de triángulo de Sierpinski
Para el modelado y el análisis, se realizó la simulación de un triángulo de Sierpinski de tercer orden en un programa de modelado que nos ayuda a analizar el comportamiento del campo magnético de la antena. Realizando iteraciones para llegar al tercer orden, como se observa en la figura.
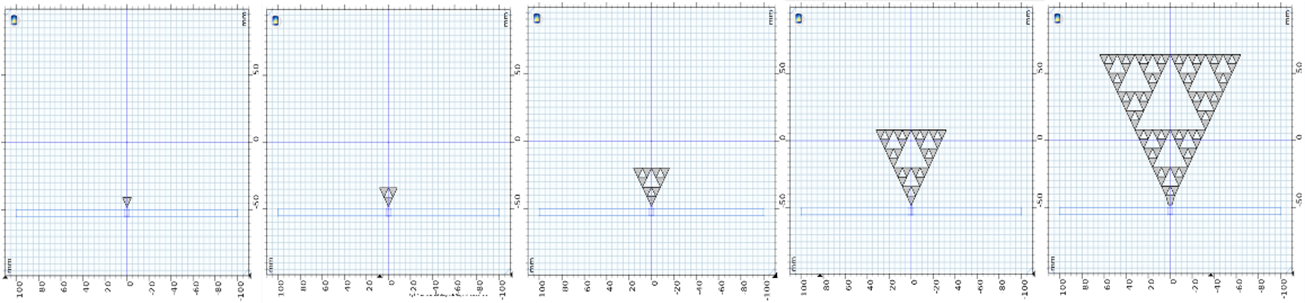
Figura 4. Construcción del triángulo de Sierpinski de tercer orden
Se coloca sobre una superficie en donde se conecta a una terminal de cable coaxial, realizando las iteraciones para llegar al tercer orden, como se observa en la figura 4. Esto para obtener el valor del campo electromagnético para esta antena y tener un punto de partida para las comparaciones posteriores. Para observar el cambio en los valores del campo magnético de la antena, se introduce una iteración al triángulo que se encuentra al centro de nuestra simulación de Sierpinski de tercer orden.

Figura 5. Triángulo de Sierpinski de tercer orden modificado
En las primeras simulaciones de la geometría fractal de tercer orden del triángulo de Sierpinski que se generaron a frecuencias reportadas dentro de la simulación de 1.6GHz y 3GHz se obtuvieron valores del orden de 3.55E-8T ,3.59E-13T (observar figura 6).

Figura 6. Simulación del campo magnético del Triángulo de Sierpinski de tercer orden
Para el caso en que la geometría fue modificada se obtuvieron valores de 2.34E-9T y 1.21E-7T (ver figura 7)
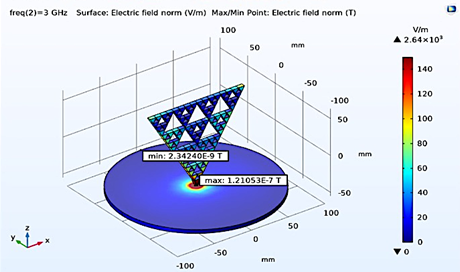
Figura 7. Simulación del campo magnético del Triángulo de Sierpinski modificado
Además de que se probó la simulación de la antena de tipo patch antenna para mejorar el análisis de estas antenas.
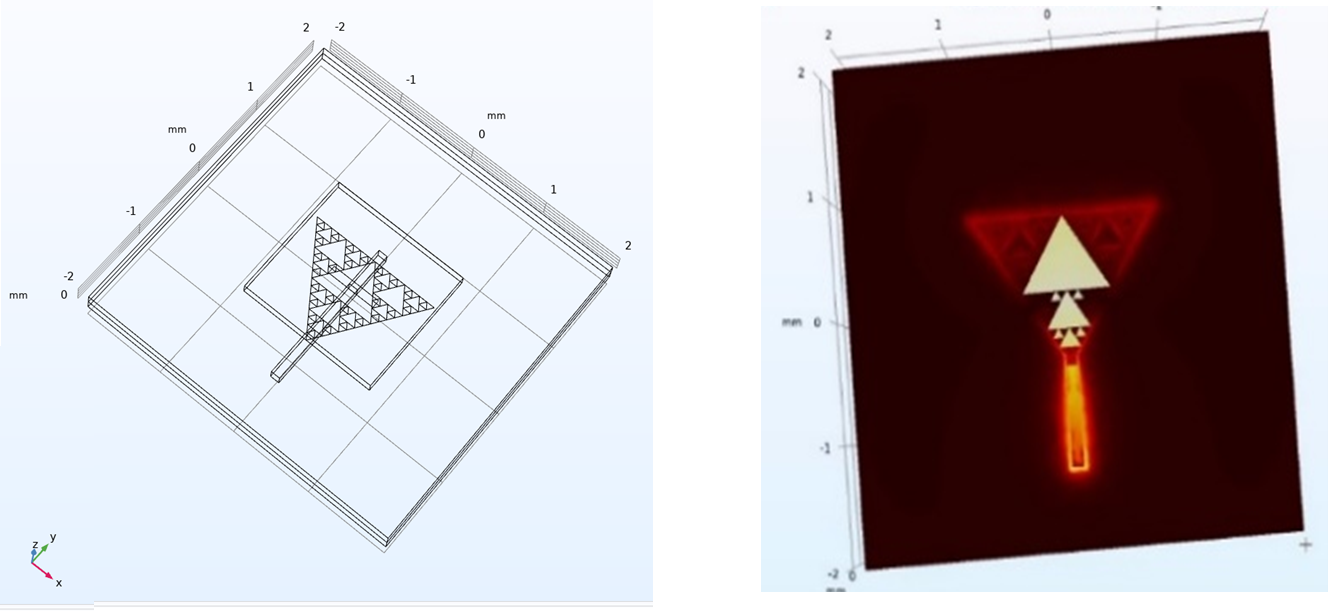
Figura 8. Antena de parche del triángulo de Sierpisnki
con un dominio de frecuencia de 30GHz (para observar el comportamiento de las antenas a una frecuencia muy alta). Se obtienen valores de campo eléctrico que van desde 1V/m hasta 5.92E10V/m.

Figura 9. Ejemplo de antena de parche expandida
Con la configuración del patrón de campo lejano y a esta frecuencia experimental muy alta, se puede apreciar de manera más sencilla cómo es que la antena de Sierpinski tiene un comportamiento de antena fractal.
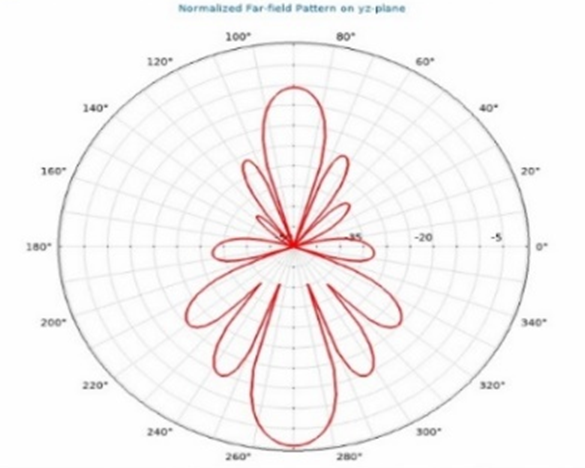
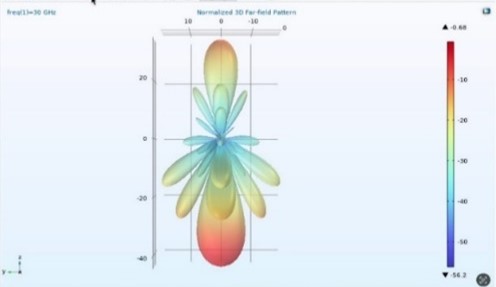
Figura 10. Configuración del patrón de campo lejano para la antena de Sierpinski de 30GHz
Mediante el uso de un programa computacional, podemos analizar las antenas fractales y determinar hasta qué número de iteraciones son funcionales. Esto nos permite evaluar si la construcción física se complicará a medida que aumenta el número de repeticiones del algoritmo. Gracias a esta herramienta, podremos realizar construcciones de antenas de manera más sencilla. Dentro de la simulación, es posible modificar varios parámetros para obtener los valores de campo deseados o aquellos ya reportados en la literatura. En este caso, hemos elegido la geometría del triángulo de Sierpinski para comprender los fundamentos de las antenas fractales, ya que son pocas las antenas que utilizan esta geometría según la literatura. Al simular estas geometrías, podemos comenzar a incorporar antenas fractales en cualquier dispositivo que se encuentre dentro del rango de las microondas y la radiofrecuencia. La construcción de antenas fractales multibanda nos brinda la oportunidad de aprovechar sus ventajas, como su tamaño compacto, lo que las hace ideales para integrar en dispositivos. Estas antenas también ofrecen funcionalidad y la capacidad de excitar múltiples frecuencias simultáneamente. Esto abre nuevas posibilidades en el campo de la medicina, mejorando los diagnósticos, la monitorización y la comunicación inalámbrica en entornos médicos. Además, podemos comparar las antenas de superficie RF con las antenas fractales para determinar cuál proporciona un campo más homogéneo tanto en frecuencia como en espacio. Esto es especialmente relevante, ya que las antenas fractales se utilizan en implantes para detectar signos vitales.